7.11.Бинарные
деревья.
7.12.Действия с бинарными деревьями.
7.13.Решение задач работы с бинарным деревом.
Кроме
линейных структур существуют и нелинейные,
при помощи которых задаются иерархические
связи данных. Для этого используются графы,
а среди них сетевые и древовидные структуры.
Рассмотрим один вид деревьев - бинарное
дерево.
Бинарное
(двоичное) дерево -
это конечное множество элементов, которое
либо пусто, либо содержит один элемент,
называемый корнем дерева, а остальные
элементы множества делятся на два
непересекающихся подмножества, каждое из
которых само является бинарным деревом. Эти
подмножества называются правым и левым
поддеревьями исходного дерева.

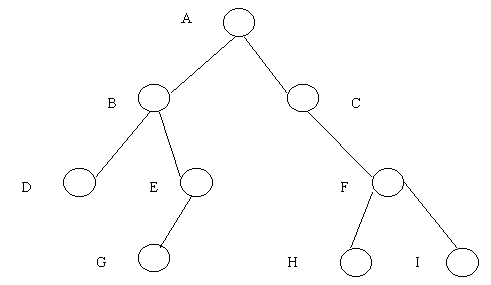
Рис.
8 Двоичное дерево
На рис. 8
показан наиболее часто встречающийся
способ представления бинарного дерева. Оно
состоит из девяти узлов. Корнем дерева
является узел А. Левое поддерево имеет
корень В, а правое поддерево - корень С. Они
соединяются соответствующими ветвями,
исходящими из А. Отсутствие ветви означает
пустое поддерево. Например, у поддерева с
корнем С нет левого поддерева, оно пусто.
Пусто и правое поддерево с корнем Е.
Бинарные поддеревья с корнями D,
G,
H
и I
имеют пустые левые и правые поддеревья.
Узел, имеющий пустые правое и левое
поддеревья, называется листом. Если каждый
узел бинарного дерева, не являющийся листом,
имеет непустые правое и левое поддеревья,
то дерево называется строго бинарным
Уровень
узла в бинарном дереве определяется
следующим образом: уровень корня всегда
равен нулю, а далее номера уровней при
движении по дереву от корня увеличиваются
на 1 по отношению к своему
непосредственному предку. Глубина
бинарного дерева - это максимальный уровень
листа дерева, иначе говоря, длина самого
длинного пути от корня к листу дерева. Узлы
дерева могут быть пронумерованы по
следующей схеме (см. рис. 9)
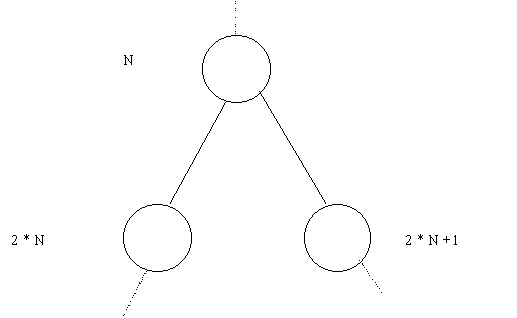
Рис. 9
Схема нумерации узлов двоичного дерева
Номер
корня всегда равен 1, левый потомок получает
номер 2, правый - номер 3. Левый потомок узла 2
должен получить номер 4, а правый - 5, левый
потомок узла 3 получит номер 6, правый - 7 и т.д.
Несуществующие узлы не нумеруются, что,
однако, не нарушает указанного порядка, так
как их номера не используются. При такой
системе нумерации в дереве каждый узел
получает уникальный номер.
Полное
бинарное дерево уровня n
- это дерево, в котором каждый узел уровня n
является листом и каждый узел уровня меньше
n
имеет непустые правое и левое поддеревья.
Почти
полное бинарное дерево определяется как
бинарное дерево, для которого существует
неотрицательное целое k
такое, что:
1)
каждый лист в дереве имеет уровень k
или k+1;
2)
если узел дерева имеет правого потомка
уровня k+1,
тогда все его левые потомки, являющиеся
листами, также имеют уровень k+1.
Рассматривая
действия над деревьями, можно сказать, что
для построения дерева необходимо
формировать узлы, и, определив
предварительно место включения,
включать их в
дерево. Количество
узлов определяется необходимостью.
Алгоритм включения должен быть известен и
постоянен. Узлы дерева могут быть
использованы для хранения какой-либо
информации.
Далее
необходимо осуществлять поиск заданного
узла в дереве. Это можно
организовать, например,
последовательно обходя узлы дерева, причем
каждый узел должен быть просмотрен только
один раз.
Может
возникнуть задача и уничтожения дерева в
тот момент, когда необходимость в нем (в
информации, записанной в его элементах)
отпадает. В ряде случаев может
потребоваться уничтожение поддерева.
Для того,
чтобы совокупность узлов образовала дерево,
необходимо каким-то образом формировать и
использовать связи узлов со своими
предками и потомками. Все это очень
напоминает действия над элементами списка.
7.12.1.
Построение бинарного дерева.
Важным
понятием древовидной структуры является
понятие двоичного дерева поиска. Правило
построения двоичного дерева поиска:
элементы, у которых значение некоторого
признака меньше, чем у корня, всегда
включаются слева от некоторого поддерева, а
элементы со значениями, большими, чем у
корня - справа. Этот принцип
используется и при формировании двоичного
дерева, и при поиске в нем элементов. Таким
образом, при поиске элемента с некоторым
значением признака происходит спуск по
дереву, начиная от корня, причем выбор ветви
следующего шага - направо или налево
согласно значению искомого признака
- происходит в каждом очередном узле на
этом пути. При поиске элемента результатом
будет либо найденный узел с заданным
значением признака, либо поиск закончится
листом с «нулевой» ссылкой, а требуемый
элемент отсутствует на проделанном по
дереву пути. Если поиск был проделан для
включения очередного узла в дерево, то в
результате будет найден узел с пустой
ссылкой (пустыми ссылками), к которому
справа или слева в соответствии со
значением признака и будет присоединен
новый узел.
Рассмотрим
пример формирования двоичного дерева.
Предположим, что нужно сформировать
двоичное дерево, узлы (элементы) которого
имеют следующие значения признака: 20, 10,
35, 15, 17, 27, 24, 8, 30. В этом же порядке они и будут
поступать для включения в двоичное дерево.
Первым узлом в дереве (корнем) станет узел
со значением 20. Обратить внимание: поиск
места подключения очередного элемента
всегда начинается с корня.
К корню слева подключается элемент 10. К
корню справа подключается элемент 35. Далее
элемент 15 подключается справа к 10, проходя
путь: корень 20 - налево - элемент 10 - направо -
подключение, так как дальше пути нет.
Процесс продолжается до исчерпания
включаемых элементов. Результат
представлен на рис. 10.
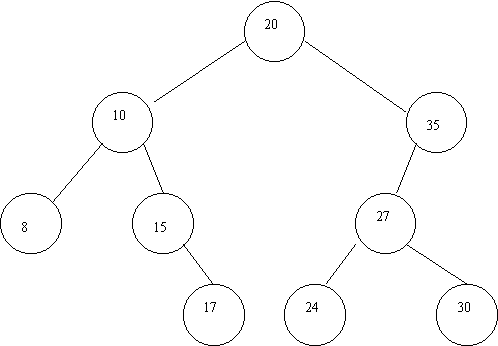
Рис. 10 Построение бинарного дерева.
Значения элементов дерева: 20, 10, 35, 15, 17, 27,
24, 8, 30
При
создании двоичного дерева отдельно
решается вопрос с возможностью включения
элементов с дублирующими признаками.
Алгоритм двоичного поиска позволяет при
включении корректно расположить узлы в
дереве, однако при поиске уже включенных
элементов возникают сложности, так как
при стандартном варианте поиска будет
выбираться только один из дублей. Для
обнаружения всех дублей должен быть
применен алгоритм такого обхода дерева, при
котором каждый узел дерева будет выбран
один раз.
Элемент
дерева используется для хранения какой-либо
информации, следовательно, он должен
содержать информационные поля, возможно
разнотипные. Элемент двоичного дерева
связан в общем случае с двумя прямыми
потомками, а при необходимости может быть
добавлена и третья связь - с
непосредственным предком. Отсюда следует,
что по структуре элемент дерева (узел) похож
на элемент списка и может быть описан так же.
Как и в списке, в дереве должна существовать
возможность доступа к его «первому»
элементу - корню дерева. Она реализуется
через необходимую принадлежность дерева -
поле ROOT, в котором записывается ссылка на
корневой элемент.
Приведем
пример описания полей и элементов,
необходимых для построения дерева.
Type
Nd = ^ node;
Node = record
Inf1 : integer;
Inf2 :
string ;
Left :
nd;
Right : nd;
End;
Var
Root, p,q : nd;
Приведенный
пример описания показывает, что описание
элемента списка и узла дерева по сути ничем
не отличаются друг от друга. Различия в
технологии действий тоже невелики -
основные действия выполняются над ссылками,
адресами узлов. Основные различия - в
алгоритмах.
При
работе с двоичным деревом возможны
следующие основные задачи:
1)
создание элемента, узла дерева,
2)
включение его в дерево по алгоритму
двоичного поиска,
3)
нахождение в дереве узла с заданным
значением ключевого признака,
4)
определение максимальной глубины
дерева,
5)
определение количества узлов
дерева,
6)
определение количества
листьев дерева,
7)
ряд других задач.
Приведем
примеры процедур, реализующих основные
задачи работы с бинарным деревом.
Procedure
CREATE_EL_T(var q:ND; nf1:integer;
inf2:string);
begin
new(q);
q^.inf1:=inf1;
q^.inf2:=inf2;
{значения
полей передаются в качестве параметров}
q^.right:=nil;
q^.left:=nil;
end;
procedure
Insert_el ( p : nd; {адрес
включаемого
элемента} var
root : nd);
var
q, t : nd;
begin
if root = nil then
root := p {элемент
стал корнем}
else
begin { поиск
по дереву
}
t
:= root;
q := root;
while ( t <> nil ) do
begin
if p^.inf1 < t^.inf1
then
begin
q := t;{ запоминание
текущего адреса}
t := t^.left; {уход
по левой ветви}
end
else
if p^.inf1 > t^.inf1 then
begin
q := t;{ запоминание
текущего адреса}
t := t^.right; {уход
по правой ветви}
end
else
begin
writeln ('найден
дубль включаемого элемента');
exit; {завершение
работы процедуры}
end
end;
{после
выхода из цикла в q - адрес элемента, к
которому должен
быть подключен новый элемент}
if
p^.inf1 < q^.inf1 then
q^.left := p {подключение
слева
}
else
q^.right := p; {подключение
справа}
end;
ПРИМЕЧАНИЕ:
элемент с дублирующим ключевым признаком в
дерево не включается.
Данный
алгоритм движения по дереву может быть
положен в основу задачи определения
максимального уровня (глубины) двоичного
дерева, определения, есть ли в дереве
элемент с заданным значением ключевого
признака и т.д., то есть таких задач, решение
которых основывается на алгоритме
двоичного поиска по дереву.
Однако не все задачи могут быть
решены с применением двоичного поиска,
например, подсчет общего числа узлов дерева.
Для этого требуется алгоритм, позволяющий
однократно посещать каждый узел дерева.
При
посещении любого узла возможно однократное
выполнение следующих трех действий:
1)
обработать узел (конкретный набор
действий при этом не важен). Обозначим это
действие через О (обработка);
2)
перейти по левой ссылке (обозначение - Л);
3)
перейти по правой ссылке (обозначение -
П).
Можно
организовать обход узлов двоичного дерева,
однократно выполняя над каждым узлом эту
последовательность действий. Действия
могут быть скомбинированы в произвольном
порядке, но он должен быть постоянным в
конкретной задаче обхода дерева.
На
примере дерева на рис. 10 проиллюстрируем
варианты обхода дерева.
1)
Обход вида ОЛП. Такой обход называется «в
прямом порядке», «в глубину». Он даст
следующий порядок посещения узлов:
20,
10, 8, 15, 17, 35, 27, 24, 30
2)
Обход вида ЛОП. Он называется «симметричным»
и даст следующий порядок посещения узлов:
8,
10, 15, 17, 20, 24, 27, 30, 35
3)
Обход вида ЛПО. Он называется «в
обратном порядке» и даст следующий порядок
посещения узлов:
8,
17, 15, 10, 24, 30, 27, 35, 20
Если
рассматривать задачи, требующие сплошного
обхода дерева, то для части из них порядок
обхода, в целом, не важен, например, подсчет
числа узлов дерева, числа листьев/не
листьев, элементов, обладающих заданной
информацией и т.д. Однако такая задача, как
уничтожение бинарного дерева с
освобождением памяти, требует
использования только обхода «в обратном
порядке».
Рассмотрим
средства, с помощью которых можно
обеспечить варианты обхода дерева.
При
работе с бинарным деревом с точки зрения
программирования оптимальным вариантом
построения программы является
использование рекурсии. Базисный вариант
рекурсивной процедуры обхода бинарного
дерева очень прост.
{ обход дерева по варианту ЛОП }
Procedure Recurs_Tree ( q : nd );
Begin
If q <> nil Then
begin
Recurs_Tree( q^.left );{уход
по
левой
ветви-Л}
Work ( q ); { процедура
обработки
дерева-О}
Recurs_Tree( q^.right );{уход
по правой ветви-П}
End;
End;
Для
практической проработки действия
механизма рекурсии при реализации
вариантов обхода дерева можно
воспользоваться уже построенным деревом с
рис.10.
Пример
использования рекурсивной процедуры при
решении задачи подсчета листьев двоичного
дерева.
Procedure Leafs_Count( q : nd; var k
: integer );
Begin
If q <> nil Then
begin
Leafs_Count( q^.left, k );
If (q^.left = nil) and (q^.right =
nil) Then
K := K +1;
Leafs_Count( q^.right, k );
End;
End;
{удаление дерева с освобождением памяти}
Procedure del_tree(q : nd );
Begin
if q<>nil then
begin
del_tree (q^.left);
del_tree (q^.right);
dispose(q)
end
end;
В
заключение следует сказать о том, что
рекурсивный обход дерева применим в
большинстве задач,
однако необходимо все же
различать варианты эффективного
применения двоичного поиска
и сплошного обхода.