7.6.Организация списков.
7.7.Задачи включения элемента в линейный
однонаправленный список без головного
элемента.
7.8.Задачи на удаление элементов из
линейного однонаправленного списка без
головного элемента.
7.9.Стеки, деки, очереди.
7.10.Использование рекурсии при работе со
списками.
Преимущества
динамической памяти становятся особенно
очевидными при организации динамических
структур, элементы которых связаны через
адреса (стеки, очереди, деревья, сети и т.д.).
Основой моделирования таких структур
являются списки.
Список -
это конечное множество динамических
элементов, размещающихся в разных
областях памяти и объединенных в
логически упорядоченную
последовательность с помощью специальных
указателей (адресов связи).
Список -
структура данных, в которой каждый элемент
имеет информационное поле (поля) и ссылку (ссылки),
то есть адрес (адреса), на другой элемент (элементы)
списка. Список - это так называемая
линейная структура данных, с помощью
которой задаются одномерные отношения.
Каждый
элемент списка содержит информационную и
ссылочную части. Порядок расположения
информационных и ссылочных полей в
элементе при его описании - по выбору
программиста, то есть фактически
произволен. Информационная часть в общем
случае может быть неоднородной, то есть
содержать поля с информацией различных
типов. Ссылки однотипны, но число их может
быть различным в зависимости от типа
списка. В связи с этим для описания
элемента списка подходит только тип «запись»,
так как только этот тип данных может иметь
разнотипные поля. Например, для
однонаправленного списка элемент должен
содержать как минимум два поля: одно поле
типа «указатель», другое - для хранения
данных пользователя. Для двунаправленного
- три поля, два из которых должны быть типа
«указатель».
Структура
элемента линейного однонаправленного
списка представлена на рисунке 1.

Следует
рассмотреть разницу в порядке обработки
элементов массива и списка.
Элементы
массива располагаются в памяти в
определенном постоянном порядке - подряд,
друг за другом, что закрепляется их
номерами. Каждый элемент массива имеет
свое место, которое не может быть изменено,
хотя значение элемента может изменяться.
Порядок обработки элементов определяется
использованием их номеров, индексов.
В отличие
от элементов массива элементы списка
могут располагаться
в памяти в свободном порядке, не подряд.
Порядок их обработки определяется
ссылками, то есть в общем случае очередной
элемент своей ссылкой указывает на тот
элемент, который должен быть обработан
следующим. Последний по порядку элемент
содержит в ссылочной части признак,
свидетельствующий о необходимости
прекращения обработки элементов списка,
указывающий как бы конец списка.
В
зависимости от числа ссылок список
называется одно-, двунаправленным и т.д.
В
однонаправленном списке каждый элемент
содержит ссылку на последующий элемент.
Если последний элемент списка содержит «нулевую»
ссылку, то есть содержит значение
предопределенной константы nil
и, следовательно, не ссылается ни на какой
другой элемент, такой список называется
линейным.
Для
доступа к первому элементу списка, а за ним
- и к последующим элементам необходимо
иметь адрес первого элемента списка. Этот
адрес обычно записывается в специальное
поле - указатель на первый элемент, дадим
ему специальное, «говорящее»
имя - first.
Если значение first
равно nil,
это значит, что список пуст, он не содержит
ни одного элемента. Оператор first
:= nil;
должен быть первым оператором в программе
работы со списками. Он выполняет
инициализацию указателя
первого элемента
списка, иначе говоря, показывает, что
список пуст. Всякое другое значение будет
означать адрес первого элемента списка (не
путать с
неинициализированным состоянием
указателя).
Структура
линейного однонаправленного списка
показана на рисунке 2.
Если
последний элемент содержит ссылку на
первый элемент списка, то такой список
называется кольцевым, циклическим.
Изменения в списке при этом минимальны -
добавляется ссылка с последнего на первый
элемент списка: в адресной части
последнего элемента значение Nil
заменяется на адрес первого
элемента списка (см.
рис. 3).
При
обработке однонаправленного списка могут
возникать трудности, связанные с тем, что
по списку с такой организацией можно
двигаться только в одном направлении, как
правило, начиная с первого элемента.
Обработка списка в обратном направлении
сильно затруднена. Для устранения этого
недостатка служит двунаправленный список,
каждый элемент которого содержит ссылки
на последующий и предыдущий элементы (для
линейных списков - кроме первого и
последнего элементов). Структура элемента
представлена на рис. 1б.


Такая
организация списка позволяет от каждого
элемента двигаться по списку как в прямом,
так и в обратном направлениях. Наиболее
удобной при этом является та организация
ссылок, при которой движение, перебор
элементов в
обратном направлении является строго
противоположным перебору элементов в
прямом направлении. В этом случае список
называется симметричным. Например, в
прямом направлении элементы линейного
списка пронумерованы и выбираются так: 1, 2,
3, 4, 5. Строго говоря, перебирать элементы в
обратном направлении можно по-разному,
соответствующим способом организуя
ссылки, например: 4, 1, 5, 3, 2. Симметричным же
будет называться список, реализующий
перебор элементов в таком порядке: 5, 4, 3, 2, 1.
Следует
заметить, что «обратный» список, так же,
как и прямой, является просто линейным
однонаправленным списком, который
заканчивается элементом со ссылкой,
имеющей значение nil.
Для удобства работы со списком в обратном
направлении и в соответствии с идеологией однонаправленного
списка нужен доступ к первому в обратном
направлении элементу. Такой доступ
осуществляется с помощью указателя LAST
на этот первый в обратном направлении
элемент. Структура линейного
двунаправленного симметричного списка
дана на рис. 4 .
Как
указывалось ранее, замкнутый, циклический,
кольцевой список
организован таким образом, что в адресную
часть конечного элемента вместо константы
nil помещается адрес начального
элемента (список замыкается на себя). В
симметричном кольцевом списке такое
положение характерно для обоих - прямого и
обратного - списков, следовательно, можно
построить циклический двунаправленный
список (см. рис. 5 ) .
Описать
элемент однонаправленного списка (см. рис
1) можно следующим образом:
type
point=^zap;
zap=record
inf1 :
integer;
{ первое информационное поле
}
inf2
: string;
{ второе информационное поле
}
next :
point;
{ссылочное поле }
end;
Из этого
описания видно, что имеет место
рекурсивная ссылка: для описания типа point
используется тип zap, а при описании типа zap используется
тип point.
По соглашениям Паскаля в этом случае
сначала описывается тип «указатель», а
затем уже тип связанной с ним переменной.
Правила Паскаля только при описании
ссылок допускают использование
идентификатора (zap) до его
описания. Во всех остальных случаях,
прежде чем упомянуть идентификатор,
необходимо его определить.


В случае
двунаправленного списка в описании должно
появиться еще одно ссылочное поле того же
типа, например:
type
point=^zap;
zap=record
inf1
: integer;
{ первое информационное поле
}
inf2
: string;
{ второе информационное поле
}
next :
point; {ссылочное
поле на следующий элемент}
prev: point;
{ссылочное поле на предыдущий элемент}
end;
Как
уже отмечалось, последовательность
обработки элементов списка задается
системой ссылок. Отсюда следует важный
факт: все действия над элементами списка,
приводящие к изменению порядка обработки
элементов списка - вставка, удаление,
перестановка - сводятся к действиям со
ссылками. Сами же элементы не меняют
своего физического положения в памяти.
При
работе со списками любых видов нельзя
обойтись без указателя на первый элемент.
Не менее полезными, хотя и не всегда
обязательными, могут стать адрес
последнего элемента списка и количество
элементов. Эти данные могут существовать
по отдельности, однако их можно объединить
в единую структуру типа «запись» (из-за
разнотипности полей: два поля указателей
на элементы и числовое поле для количества
элементов). Эта структура и будет
представлять так называемый головной
элемент списка. Следуя идеологии
динамических структур данных, головной
элемент списка также необходимо сделать
динамическим, выделяя под него память при
создании списка и освобождая после
окончания работы. Использование данных
головного элемента делает работу со
списком более удобной, но требует
определенных действий по его обслуживанию.
Рассмотрим
основные процедуры работы с линейным
однонаправленным списком без головного
элемента. Действия оформлены в виде
процедур или функций в соответствии с
основными требованиями модульного
программирования (см. соответствующий
раздел пособия).
Приведем
фрагменты разделов Type
и Var,
необходимые для дальнейшей работы с
линейным однонаправленным списком без
головного элемента.
type
el = ^zap;
zap=record
inf1
: integer; { первое информационное поле
}
inf2
: string;
{ второе информационное поле
}
next : el;
{ссылочное поле }
end;
VAR
first,
{
указатель на первый элемент списка }
p, q , t : el;
{ рабочие указатели, с помощью которых будет
выполняться работа с элементами
списка }
наверх
Графическое
представление выполняемых действий
дано на рис. 6

Procedure
Create_Empty_List ( var first :
el);
Begin
first = nil;
End;
Procedure
Create_New_Elem(var p: el);
BEGin
New (p);
Writeln ('введите
значение первого информационного поля:
');
Readln
( p^.inf1 );
Writeln ('введите
значение второго информационного поля:
'); Readln
( p^.inf2
);
p^.next
:= nil;
{ все
поля элемента должны быть
инициализированы }
End;
7.7.3.
Подсчет числа элементов списка.
Function
Count_el(First:el):integer;
Var
K : integer;
q : el;
Begin
If First = Nil then
k:=0
{ список
пуст }
Else
begin
{список
существует}
k:=1; {в
списке есть хотя бы один элемент}
q:=First; {перебор
элементов списка начинается
с первого}
While
q^.Next <> Nil do
Begin
k:=k+1;
q:=q^.Next; {переход
к следующему элементу списка}
End;
End;
Count_el:=k;
End;
ПРИМЕЧАНИЕ:
аналогично может быть написана процедура,
например, печати списка, поиска адреса
последнего элемента и др.
7.7.4.
Вставка элемента в начало списка.
Procedure
Ins_beg_list(P : el; {адрес включаемого
элемента}
Var First : el);
Begin
If First = Nil Then
begin
First := p;
P^.next := nil { можно
не делать, так как уже сделано при формировании этого элемента}
end
Else
Begin
First:=p;{
включаемый элемент
становится первым }
P^.Next:=First;{ссылка
на бывший первым элемент}
End;
End;
Procedure
Ins_end_list(P : el; Var First : el);
Begin
If First = Nil Then
First:=p
Else
Begin
q:=First; {цикл
поиска адреса последнего элемента}
While
q^.Next <> Nil do
q:=q^.Next;
q^.Next:=p;{ссылка
с бывшего последнего
на
включаемый элемент}
P^.Next:=Nil; {не обязательно}
End;
End;
7.7.6.
Включение в середину (после i-ого
элемента).
Procedure
Ins_after_I ( first : el; p : el; i : integer);
Var
t, q : el;
K ,n : integer;
Begin
n
:= count_el(first);
{определение числа элементов списка}
if (i < 1 ) or ( i >
n )then
begin
writeln ('i
задано некорректно');
exit;
end
else
begin
if i = 1 then
begin
t := first;{адрес 1 элемента}
q := t^.next; {адрес 2 элемента}
t^.next := p;
p^.next := q;
end
ELSe
if i = n then
begin
{ см. случай вставки после
последнего элемента}
.
. .
end
else
{вставка в «середину» списка}
begin
t := first;
k := 1;
while ( k < i ) do
begin
{поиск адреса i-го
элемента}
k
:= k + 1;
t := t^.next;
end;
q := t^.next;
{найдены адреса
i-го (t)
и i+1
-го (q) элементов }
t^.next := p;
p^.next := q;
{элемент с
адресом р вставлен}
end;
end;
End;
ПРИМЕЧАНИЕ:
аналогично рассуждая и применяя
графическое представление действия, можно
решить задачу включения элемента перед i-ым.
Строго говоря, такая задача не
эквивалентна задаче включения элемента
после (i-1)-го.
наверх
7.8.
Задачи на удаление элементов из
линейного однонаправленного списка без
головного элемента.
Графическое
представление выполняемых действий дано
на рисунке 7.
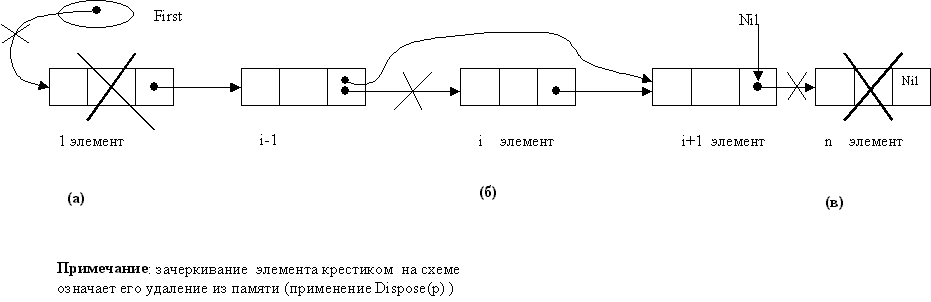
ПРИМЕЧАНИЕ:
перед выполнением операции удаления
элемента или списка желательно
запрашивать у пользователя подтверждение
удаления.
Procedure Del_beg_list ( Var First
: el);
Var
p : el;
answer : string;
Begin
If First <> Nil then
Begin
{ список не
пуст }
writeln
('Вы хотите
удалить первый элемент?(да/нет)
');
readln
( answer );
if answer = 'да'
then
begin
p:=First;
If p^.Next = Nil Then {в
списке один элемент
}
Begin
Dispose (p); {уничтожение
элемента}
First:=Nil; {список стал пустым
}
End
Else
Begin
P
:= first;
{адрес
удаляемого элемента
}
First:=first^.Next;
{адрес нового первого элемента}
Dispose(p);
{удаление бывшего первого элемента
}
End;
End
end
Else
writeln
(' список пуст,
удаление первого элемента невозможно');
End;
Нужен
запрос на удаление
Procedure Del_end_list( Var First :el);
Begin
If First <> Nil then
Begin {список
не пуст}
if
fist^.next = nil then
begin
{в списке - единственный элемент
}
p
:= first;
dispose (p);
First := nil;
End
Else
begin
{в списке больше одного элемента
}
Q
:= First;
T := First;
{цикл
поиска адреса последнего элемента}
While q^.Next <> Nil do
Begin
T
:= q;{запоминание
адреса текущего
элемента}
q:=q^.Next;{переход
к следующему
элементу}
end;
{после
окончания цикла Т - адрес предпоследнего, а Q - адрес последнего элемента списка}
dispose
(q);
{удаление последнего элемента}
t^.next
:= nil;
{предпоследний элемент стал последним}
end
end
else
writeln
('список пуст, удаление элемента
невозможно
');
END;
ПРИМЕЧАНИЕ.
После исключения элемента из списка этот
элемент может не
удаляться из памяти, а через список
параметров передан на какую-либо обработку,
если этого требует алгоритм
обработки данных.
Procedure Del_I_elem ( first : el; i
: integer);
Var
t, q, r : el;
K ,n : integer;
Begin
n
:= count_el(first);
{определение числа элементов списка}
if (i < 1 ) or ( i >
n ) then
begin
writeln ('i
задано некорректно');
exit;
end
else
begin
{нужно добавить подтверждение
удаления
}
if
i = 1 then
begin {удаляется
1 элемент}
t := first;
first:= first^.next;
dispose ( t);
end
else
if i = n then
begin
{ см. случай удаления последнего
элемента}
.
. .
end
else
{удаление из «середины» списка}
begin
t := first;
q := nil;
k := 1;
while ( k < i ) do
begin {поиск
адресов (i-1)-го
и i-го элементов}
k
:= k + 1;
q := t;
t := t^.next;
end;
r := t^.next;
{найдены
адреса i-го (t),
(i-1)-го (q) и (i+1)-го
(r) элементов
}
q^.next
:= r;
dispose ( t ); {удален
i-ый элемент
}
end;
end;
ENd;
Procedure
Delete_List(Var First : el);
Var
P, q : el;
Answer : string;
Begin
If First <> Nil Then
Begin
{ список не
пуст }
writeln
( ' Вы хотите
удалить весь список ? (да/нет)'
);
readln
( answer );
if answer = 'да'
then
begin
q:=First;
p:=nil;
While ( q <> nil ) do
Begin
p:=q;
q:=q^.Next;
Dispose(p);
End;
First:=Nil;
End;
End
Else
writeln ('список
пуст
');
End;
Операция
замены элемента в списке практически
представляет собой комбинацию удаления и
вставки элемента. Читателю дается
возможность, используя представленные
ранее графические приемы и примеры
программ, самому написать процедуры замены
элементов. Перед выполнением операции
замены элемента
желательно запрашивать у пользователя
подтверждение замены.
Действуя
аналогично, можно построить графические
схемы и программы задач действий с
двунаправленными списками.
наверх
7.9.
Стеки, деки, очереди.
Одной
из важных концепций
в программировании является концепция
стека. Стеком называется упорядоченный
набор элементов, в котором добавление новых
элементов и удаление существующих
выполняется только с одного его конца,
который называется вершиной стека.
Бытовой иллюстрацией стека может служить
стопка книг. Добавить к ней очередную книгу
можно, положив новую поверх остальных.
Верхняя книга (элемент стека) и есть
вершина стека. Просматривать книги можно
только по одной, снимая их с вершины. Чтобы
получить книгу из середины стека, надо
задать критерий отбора и удалять элементы-книги
из стека до тех пор, пока не будет найдена
нужная книга. Элементы из стека могут
удаляться, пока он не станет пустым. Таким
образом, над стеком выполняются следующие
операции:
1)
добавление в стек нового элемента;
2)
определение пуст ли стек;
3)
доступ к последнему включенному
элементу, вершине стека;
4)
исключение из стека последнего
включенного элемента.
Отсюда
ясно виден принцип работы со стеком: «пришел
последним - ушел первым»
(last
in
- first
out,
LIFO).
Такая
структура данных очень хорошо реализуется
с помощью списка. Тип списка при этом может
быть выбран в соответствии с потребностями
алгоритма. Например, для стека может
подойти линейный однонаправленный список
без головного элемента со вставкой и
исключением элементов в начале списка (это
и будет вершиной стека).
Другим
специальным видом использования списка
является очередь. Существуют различные
разновидности очередей, здесь будет
рассмотрена простая бесприоритетная
очередь. При этом добавление элементов
производится в конец очереди, а выборка и
удаление элементов -
из начала. Принцип доступа к очереди – «первым
пришел - первым ушел» (first
in
- first
out,
FIFO).
Принцип обработки как для стека, так и для
очереди определяет набор соответствующих
процедур. Для реализации очереди необходим
список, для которого известны адрес первого
и адрес последнего элементов. Таким образом,
над очередью выполняются следующие
операции:
1)
добавление в конец очереди нового
элемента;
2)
определение пуста ли очередь;
3)
доступ к первому элементу очереди;
4)
исключение из очереди первого элемента.
Эти
операции могут быть взяты из стандартного
набора действий со списком.
Кроме
рассмотренных очереди и стека есть ещё и
третий вариант структуры данных - дек,
очередь с двойным доступом, или, как ещё его
называют, - двухконечный стек. Для дека
добавление элементов, доступ к «вершине» и
удаление элемента возможны с обоих концов
списка.
наверх
7.10.
Использование рекурсии при работе со
списками.
Рекурсия
является одним из удобнейших средств при
работе с линейными списками. Она позволяет
сократить код программы и сделать
алгоритмы обхода узлов деревьев и
списков более понятными.
По
определению понятия, рекурсивная процедура
- это процедура, в
теле которой есть обращение к самой себе.
Для того, чтобы процесс рекурсии не стал
бесконечным и не вызвал переполнение стека,
в каждой рекурсивной процедуре должен быть
определен ограничитель
рекурсии, блокирующий дальнейшее «размножение»
тела процедуры.
Хотя
рекурсии в списках не являются настолько
очевидным решением, как в деревьях, все же
они позволяют оптимизировать обработку
линейных списков. В списках возможны два
варианта прохода: из начала в конец и из
конца в начало. Эти методы реализуются
очень легко в случае с двунаправленными
списками.
Рекурсию
в линейных списках демонстрирует следующий
пример: подсчет числа элементов в линейном
однонаправленном списке.
Procedure Count_Elem (var q,addr : El;
var count:integer);
Begin
if q<>nil
{ ограничитель
рекурсии
} then
begin
inc(count);
Count_El( q^.next , count);
end
End;
При
входе в процедуру count = 0 ,а q=first (указатель
на первый элемент списка).
Далее рекурсивная процедура работает так.
Анализируется значение указателя,
переданного в процедуру. Если он не равен Nil
(список не закончился), то счетчик числа
элементов увеличивается на 1. Далее
происходит очередной вызов рекурсивной
процедуры уже с адресом следующего
элемента списка, а «текущая» рекурсивная
процедура приостанавливается до окончания
вызванной процедуры. Вызванная процедура
работает точно так же: считает, вызывает
процедуру и переходит в состояние ожидания.
Формируется как бы последовательность из
процедур, каждая из которых ожидает
завершения вызванной процедуры. Этот
процесс продолжается до тех пор, пока
очередное значение адреса не станет равным
Nil (признак окончания списка). В последней
вызванной рекурсивной процедуре уже не
происходит очередного вызова,
так как не соблюдается условие q<>nil,
срабатывает «ограничитель рекурсии». В
результате процедура завершается без
выполнения каких-либо действий, а
управление возвращается в «предпоследнюю»,
вызывающую процедуру. Точкой возврата
будет оператор, стоящий за вызовом
процедуры, в данном тексте - End, и «предпоследняя»
процедура завершает свою работу, возвращая
управление в вызвавшую её процедуру.
Начинается процесс «сворачивания» цепочки
ожидающих завершения процедур. Счетчик count,
вызывавшийся по ссылке, сохраняет
накопленное значение после
завершения всей цепочки вызванных
рекурсивных процедур.
Если из текста рассмотренной процедуры
убрать использование счетчика, то
получится некий базисный вариант
рекурсивной процедуры, который можно
применять при решении других задач
обработки списка: распечатать содержимое
списка; определить, есть ли в списке элемент
с заданным порядковым номером или
определенным значением информационного
поля; уничтожить список с освобождением
памяти и др.
наверх
к
следующей части






